Fluid instability mechanisms and conditions

Squire’s theorem

Squire’s theorem states that for flows governed by the incompressible Navier-Stokes equations, the perturbations of a two-dimensional flow which are least stable are also two-dimensional.

One-dimensional shear \(U(z)\), inflection point theorem

Rayleigh’s equation (inviscid Orr-Sommerfeld equation).

(1)\[\varphi'' - k^2 \varphi - \frac{U''}{U-c} \varphi = 0\]

Derivation

We start from the inviscid Navier-Stokes equation

\[{\text{D}_t}{\boldsymbol{v}}= - {\boldsymbol{\nabla}}p\]

Two-dimensional perturbation around a shear: \({\boldsymbol{v}}= (U(z) + u, 0, w)\).

\[\begin{split} \begin{aligned} ({\partial}_t + U{\partial}_x) u + w U' &= -{\partial}_x p \\ ({\partial}_t + U{\partial}_x) w &= -{\partial}_z p. \end{aligned} \end{split}\]

We eliminate the pressure:

\[({\partial}_t + U{\partial}_x) ({\partial}_z u - {\partial}_x w) + w U'' = 0\]

This is actually the equation for the \(y\) component of the vorticity \(\omega = {\partial}_x w - {\partial}_z u\).

The flow is incompressible and 2d so we can use a streamfunction \(\psi\) such as \(u = {\partial}_z \psi\) and \(w = -{\partial}_x\psi\). The vorticity is equal to \(\omega = - ({\partial}_{xx} + {\partial}_{zz}) \psi\), which gives:

\[({\partial}_t + U{\partial}_x) ({\partial}_{xx} + {\partial}_{zz}) \psi - {\partial}_x\psi U'' = 0\]

Let’s use the symmetries of the problem with time and \(x\) so every function can be written using the Fourier transform:

\[\psi = {\mathcal{R}}( \varphi e^{ik(x- ct)}),\]

with \(k\) a real wavenumber and \(c\) a complex speed. We can replace the operators \({\partial}_t\) and \({\partial}_x\) by \(-ikc\) and \(ik\), respectively and we obtain the Rayleigh equation (1).

Theorems

\[\int_{-\infty}^{+\infty} dz \Big( \varphi'' \varphi^* - k^2 |\varphi|^2 - \frac{U''}{U-c} |\varphi|^2 \Big) = 0\]

Integration by part + limit conditions:

\[- \int_{-\infty}^{+\infty} dz \Big( |\varphi'|^2 + k^2 |\varphi|^2 \Big) = \int_{-\infty}^{+\infty} dz \Big( \frac{U''}{U-c} |\varphi|^2 \Big) < 0\]

The right hand side term can also be written as

\[\int_{-\infty}^{+\infty} dz \Big( \frac{(U-c^*)U''}{|U-c|^2} |\varphi|^2 \Big),\]

so we obtain two conditions

\[c_i \int_{-\infty}^{+\infty} dz \Big( \frac{U''}{|U-c|^2} |\varphi|^2 \Big) = 0,\]

and

\[\int_{-\infty}^{+\infty} dz \Big( \frac{(U-c_r)U''}{|U-c|^2} |\varphi|^2 \Big) < 0\]

We first conclude from the first quantity that such shear can be linearly unstable only if \(U''(z_i)\) changes sign (i.e. if the profile has an inflection point).

One can infer from the two conditions a more restrictive version that states that a velocity profile that has an inflection point \(z_i\) can be linearly unstable only if \(U''(y) (U(y) - U(y_i)) < 0\).

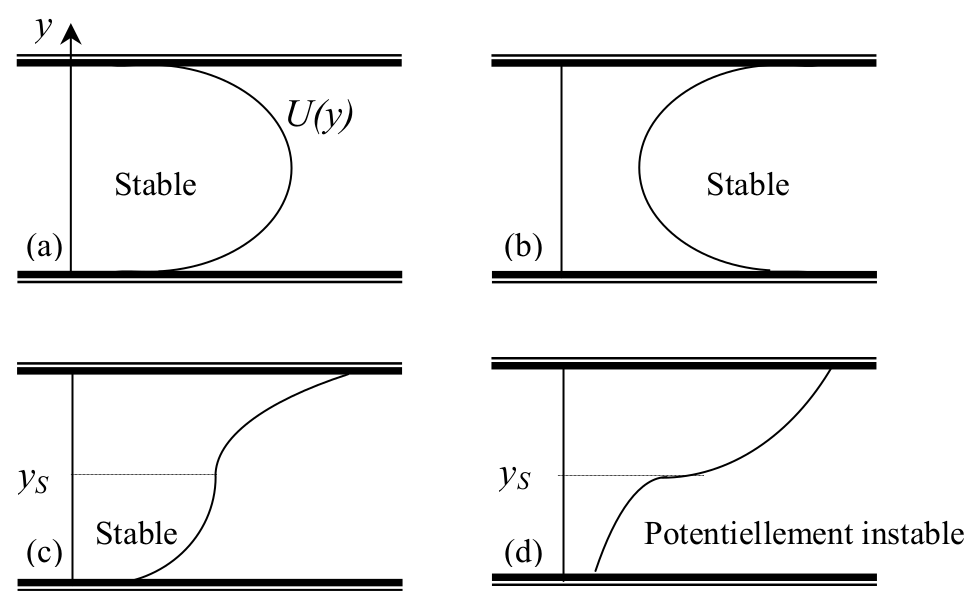
Fig. 8 Stability for different velocity profiles. There is no inflection point in (a) and (b) so these profiles are stable. (c) has a inflection point but is stable since \(U''(y) (U(y) - U(y_i)) > 0\). (d) could be unstable.

Note

Flow in a tube, Reynolds experiment and sub-critical instability…

Centrifugal instability (Rayleigh criterion)

Flows with curved streamlines, such as those sketched in Fig. 9, can be unstable due to the centrifugal force. There is a simple inviscid criterion for the instability of a basic swirling flow with an arbitrary dependence of angular velocity \(\Omega(r)\) on the distance \(r\) from the axis of rotation (\(u_\theta = r\Omega\)). The centrifugal instability can develop if

(2)\[\Phi(r) < 0 \quad \text{where} \quad \Phi(r) \equiv \frac{1}{r^3}\frac{d}{dr} \Big( r^4 \Omega^2 \Big).\]

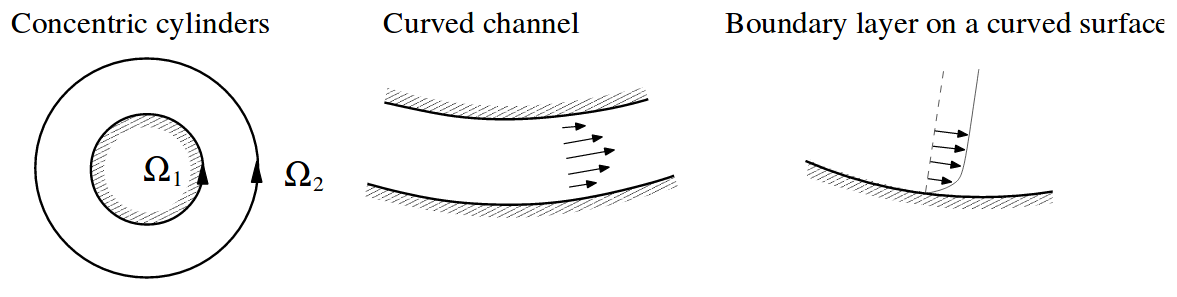
Fig. 9 Examples of swirling flows.

This criterion can be explained by considering the Euler equations for a bidimensional (\(w=0\) and \({\partial}_z = 0\)) incompressible flow expressed in cylindrical coordinates:

(3)\[\begin{split}\begin{aligned} {\text{D}_t}u_r - \frac{{u_\theta}^2}{r} &= - {\partial}_r p, \\ {\text{D}_t}u_\theta + \frac{u_r u_\theta}{r} &= - \frac{1}{r} {\partial}_\theta p, \end{aligned}\end{split}\]

where the material derivative is

(4)\[{\text{D}_t}= {\partial}_t + u_r{\partial}_r + \frac{u_\theta}{r} {\partial}_\theta.\]

The continuity equation is

\[{\partial}_r u_r + \frac{u_r}{r} + \frac{1}{r} {\partial}_\theta u_\theta = 0. \label{eqconticylindrical}\]

The equation for the vorticity is:

\[{\text{D}_t}{\boldsymbol{\omega}}= {\boldsymbol{\omega}}\cdot {\boldsymbol{\nabla}}{\boldsymbol{u}}.\]

Show that this leads to a simple equation for the vertical component of the vorticity \({\text{D}_t}\omega_z\).

Exercise 3

How should we obtain these equations?

Energetic argument

Using (3) and (4), it can be shown that the angular momentum \(H = r u_\theta\) is conserved along the trajectory of a fluid particle \( {\text{D}_t}(r u_\theta) = 0\).

The kinetic energy per mass unit is equal to \((H/r)^2/2\). We consider two fluid particles with equal volume. The sum of their kinetic energy is

\[ \frac{2 E_K}{dV} = \frac{{H_1}^2}{{r_1}^2} + \frac{{H_2}^2}{{r_2}^2}. \]

Let’s consider the swaps of the positions of the 2 particles. The new kinetic energy is

\[\frac{2 E_{K\text{new}}}{dV} = \frac{{H_1}^2}{{r_2}^2} + \frac{{H_2}^2}{{r_1}^2}.\]

The difference can be written as

\[\frac{2 (E_{K\text{new}} - E_K)}{dV} = ({H_2}^2 - {H_1}^2) \Big( \frac{1}{{r_1}^2} - \frac{1}{{r_2}^2} \Big).\]

If the swap has released energy (\(\Delta E < 0\), \({H_1}^2 > {H_2}^2\)), the laminar base flow will be unstable to such swaps. Thus the criterion is

\[\frac{dH^2}{dr} < 0 \quad \text{for instability.}\]

Recalling that \(H = r^2 \Omega\), the condition for instability as a function of \(r\) and \(\Omega\) is

\[\frac{d}{dr}(r^4 \Omega^2) < 0 \quad \text{for instability,}\]

which is consistent with the Rayleigh criterion (2).